# Week28-2 ### Association Rule Learning Association rule learning is a type of unsupervised learning technique that checks for the dependency of one data item on another data item and maps accordingly so that it can be more profitable. It tries to find some interesting relations or associations among the variables of dataset. It is based on different rules to discover the interesting relations between variables in the database. The association rule learning is one of the very important concepts of [machine learning](https://www.javatpoint.com/machine-learning), and it is employed in **Market Basket analysis, Web usage mining, continuous production, etc.** Here market basket analysis is a technique used by the various big retailer to discover the associations between items. We can understand it by taking an example of a supermarket, as in a supermarket, all products that are purchased together are put together. For example, if a customer buys bread, he most likely can also buy butter, eggs, or milk, so these products are stored within a shelf or mostly nearby. Consider the below diagram:![Association Rule Learning](https://static.javatpoint.com/tutorial/machine-learning/images/association-rule-learning.png) Association rule learning can be divided into three types of algorithms: 1. **Apriori** 2. **Eclat** 3. **F-P Growth Algorithm** We will understand these algorithms in later chapters. ### How does Association Rule Learning work? Association rule learning works on the concept of If and Else Statement, such as if A then B.![Association Rule Learning](https://static.javatpoint.com/tutorial/machine-learning/images/association-rule-learning2.png) Here the If element is called **antecedent**, and then statement is called as **Consequent**. These types of relationships where we can find out some association or relation between two items is known *as single cardinality*. It is all about creating rules, and if the number of items increases, then cardinality also increases accordingly. So, to measure the associations between thousands of data items, there are several metrics. These metrics are given below: * **Support** * **Confidence** * **Lift** **Let's understand each of them:** #### Support Support is the frequency of A or how frequently an item appears in the dataset. It is defined as the fraction of the transaction T that contains the itemset X. If there are X datasets, then for transactions T, it can be written as:![Association Rule Learning](https://static.javatpoint.com/tutorial/machine-learning/images/association-rule-learning3.png) #### Confidence Confidence indicates how often the rule has been found to be true. Or how often the items X and Y occur together in the dataset when the occurrence of X is already given. It is the ratio of the transaction that contains X and Y to the number of records that contain X.![Association Rule Learning](https://static.javatpoint.com/tutorial/machine-learning/images/association-rule-learning4.png) #### Lift It is the strength of any rule, which can be defined as below formula:![Association Rule Learning](https://static.javatpoint.com/tutorial/machine-learning/images/association-rule-learning5.png) It is the ratio of the observed support measure and expected support if X and Y are independent of each other. It has three possible values: * If **Lift= 1**: The probability of occurrence of antecedent and consequent is independent of each other. * **Lift>1**: It determines the degree to which the two itemsets are dependent to each other. * **Lift<1**: It tells us that one item is a substitute for other items, which means one item has a negative effect on another. ### Types of Association Rule Lerning Association rule learning can be divided into three algorithms: #### Apriori Algorithm This algorithm uses frequent datasets to generate association rules. It is designed to work on the databases that contain transactions. This algorithm uses a breadth-first search and Hash Tree to calculate the itemset efficiently. It is mainly used for market basket analysis and helps to understand the products that can be bought together. It can also be used in the healthcare field to find drug reactions for patients. #### Eclat Algorithm Eclat algorithm stands for **Equivalence Class Transformation**. This algorithm uses a depth-first search technique to find frequent itemsets in a transaction database. It performs faster execution than Apriori Algorithm. #### F-P Growth Algorithm The F-P growth algorithm stands for **Frequent Pattern**, and it is the improved version of the Apriori Algorithm. It represents the database in the form of a tree structure that is known as a frequent pattern or tree. The purpose of this frequent tree is to extract the most frequent patterns. ### Applications of Association Rule Learning It has various applications in machine learning and data mining. Below are some popular applications of association rule learning: * **Market Basket Analysis:** It is one of the popular examples and applications of association rule mining. This technique is commonly used by big retailers to determine the association between items. * **Medical Diagnosis:** With the help of association rules, patients can be cured easily, as it helps in identifying the probability of illness for a particular disease. * **Protein Sequence:** The association rules help in determining the synthesis of artificial Proteins. * It is also used for the **Catalog Design** and **Loss-leader Analysis** and many more other applications. {% embed url="" %} ## Clustering in Machine Learning Clustering or cluster analysis is a machine learning technique, which groups the unlabelled dataset. It can be defined as ***"A way of grouping the data points into different clusters, consisting of similar data points. The objects with the possible similarities remain in a group that has less or no similarities with another group."*** It does it by finding some similar patterns in the unlabelled dataset such as shape, size, color, behavior, etc., and divides them as per the presence and absence of those similar patterns. It is an [unsupervised learning](https://www.javatpoint.com/unsupervised-machine-learning) method, hence no supervision is provided to the algorithm, and it deals with the unlabeled dataset. After applying this clustering technique, each cluster or group is provided with a cluster-ID. ML system can use this id to simplify the processing of large and complex datasets. The clustering technique is commonly used for **statistical data analysis.** **Note: Clustering is somewhere similar to the classification algorithm, but the difference is the type of dataset that we are using. In classification, we work with the labeled data set, whereas in clustering, we work with the unlabelled dataset.** **Example**: Let's understand the clustering technique with the real-world example of Mall: When we visit any shopping mall, we can observe that the things with similar usage are grouped together. Such as the t-shirts are grouped in one section, and trousers are at other sections, similarly, at vegetable sections, apples, bananas, Mangoes, etc., are grouped in separate sections, so that we can easily find out the things. The clustering technique also works in the same way. Other examples of clustering are grouping documents according to the topic. The clustering technique can be widely used in various tasks. Some most common uses of this technique are: * Market Segmentation * Statistical data analysis * Social network analysis * Image segmentation * Anomaly detection, etc. Apart from these general usages, it is used by the **Amazon** in its recommendation system to provide the recommendations as per the past search of products. **Netflix** also uses this technique to recommend the movies and web-series to its users as per the watch history. The below diagram explains the working of the clustering algorithm. We can see the different fruits are divided into several groups with similar properties.![Clustering in Machine Learning](https://static.javatpoint.com/tutorial/machine-learning/images/clustering-in-machine-learning.png) ### Types of Clustering Methods The clustering methods are broadly divided into **Hard clustering** (datapoint belongs to only one group) and **Soft Clustering** (data points can belong to another group also). But there are also other various approaches of Clustering exist. Below are the main clustering methods used in Machine learning: 1. **Partitioning Clustering** 2. **Density-Based Clustering** 3. **Distribution Model-Based Clustering** 4. **Hierarchical Clustering** 5. **Fuzzy Clustering** #### Partitioning Clustering It is a type of clustering that divides the data into non-hierarchical groups. It is also known as the **centroid-based method**. The most common example of partitioning clustering is the [**K-Means Clustering algorithm**](https://www.javatpoint.com/k-means-clustering-algorithm-in-machine-learning). In this type, the dataset is divided into a set of k groups, where K is used to define the number of pre-defined groups. The cluster center is created in such a way that the distance between the data points of one cluster is minimum as compared to another cluster centroid. ![Clustering in Machine Learning](https://static.javatpoint.com/tutorial/machine-learning/images/clustering-in-machine-learning2.png) #### Density-Based Clustering The density-based clustering method connects the highly-dense areas into clusters, and the arbitrarily shaped distributions are formed as long as the dense region can be connected. This algorithm does it by identifying different clusters in the dataset and connects the areas of high densities into clusters. The dense areas in data space are divided from each other by sparser areas. These algorithms can face difficulty in clustering the data points if the dataset has varying densities and high dimensions.![Clustering in Machine Learning](https://static.javatpoint.com/tutorial/machine-learning/images/clustering-in-machine-learning3.png) #### Distribution Model-Based Clustering In the distribution model-based clustering method, the data is divided based on the probability of how a dataset belongs to a particular distribution. The grouping is done by assuming some distributions commonly **Gaussian Distribution**. The example of this type is the **Expectation-Maximization Clustering algorithm** that uses Gaussian Mixture Models (GMM).![Clustering in Machine Learning](https://static.javatpoint.com/tutorial/machine-learning/images/clustering-in-machine-learning4.png) #### Hierarchical Clustering Hierarchical clustering can be used as an alternative for the partitioned clustering as there is no requirement of pre-specifying the number of clusters to be created. In this technique, the dataset is divided into clusters to create a tree-like structure, which is also called a **dendrogram**. The observations or any number of clusters can be selected by cutting the tree at the correct level. The most common example of this method is the **Agglomerative Hierarchical algorithm**. ![Clustering in Machine Learning](https://static.javatpoint.com/tutorial/machine-learning/images/clustering-in-machine-learning5.png) #### Fuzzy Clustering [Fuzzy](https://www.javatpoint.com/fuzzy-logic) clustering is a type of soft method in which a data object may belong to more than one group or cluster. Each dataset has a set of membership coefficients, which depend on the degree of membership to be in a cluster. **Fuzzy C-means algorithm** is the example of this type of clustering; it is sometimes also known as the Fuzzy k-means algorithm. ### Clustering Algorithms The Clustering algorithms can be divided based on their models that are explained above. There are different types of clustering algorithms published, but only a few are commonly used. The clustering algorithm is based on the kind of data that we are using. Such as, some algorithms need to guess the number of clusters in the given dataset, whereas some are required to find the minimum distance between the observation of the dataset. Here we are discussing mainly popular Clustering algorithms that are widely used in machine learning: 1. **K-Means algorithm:** The k-means algorithm is one of the most popular clustering algorithms. It classifies the dataset by dividing the samples into different clusters of equal variances. The number of clusters must be specified in this algorithm. It is fast with fewer computations required, with the linear complexity of **O(n).** 2. **Mean-shift algorithm:** Mean-shift algorithm tries to find the dense areas in the smooth density of data points. It is an example of a centroid-based model, that works on updating the candidates for centroid to be the center of the points within a given region. 3. **DBSCAN Algorithm:** It stands **for Density-Based Spatial Clustering of Applications with Noise**. It is an example of a density-based model similar to the mean-shift, but with some remarkable advantages. In this algorithm, the areas of high density are separated by the areas of low density. Because of this, the clusters can be found in any arbitrary shape. 4. **Expectation-Maximization Clustering using GMM:** This algorithm can be used as an alternative for the k-means algorithm or for those cases where K-means can be failed. In GMM, it is assumed that the data points are Gaussian distributed. 5. **Agglomerative Hierarchical algorithm:** The Agglomerative hierarchical algorithm performs the bottom-up hierarchical clustering. In this, each data point is treated as a single cluster at the outset and then successively merged. The cluster hierarchy can be represented as a tree-structure. 6. **Affinity Propagation:** It is different from other clustering algorithms as it does not require to specify the number of clusters. In this, each data point sends a message between the pair of data points until convergence. It has O(N2T) time complexity, which is the main drawback of this algorithm. ### Applications of Clustering Below are some commonly known applications of clustering technique in Machine Learning: * **In Identification of Cancer Cells:** The clustering algorithms are widely used for the identification of cancerous cells. It divides the cancerous and non-cancerous data sets into different groups. * **In Search Engines:** Search engines also work on the clustering technique. The search result appears based on the closest object to the search query. It does it by grouping similar data objects in one group that is far from the other dissimilar objects. The accurate result of a query depends on the quality of the clustering algorithm used. * **Customer Segmentation:** It is used in market research to segment the customers based on their choice and preferences. * **In Biology:** It is used in the biology stream to classify different species of plants and animals using the image recognition technique. * **In Land Use:** The clustering technique is used in identifying the area of similar lands use in the GIS database. This can be very useful to find that for what purpose the particular land should be used, that means for which purpose it is more suitable. {% embed url="" %} ## K-Means Clustering Algorithm K-Means Clustering is an unsupervised learning algorithm that is used to solve the clustering problems in machine learning or data science. In this topic, we will learn what is K-means clustering algorithm, how the algorithm works, along with the Python implementation of k-means clustering. ### What is K-Means Algorithm? K-Means Clustering is an [Unsupervised Learning algorithm](https://www.javatpoint.com/unsupervised-machine-learning), which groups the unlabeled dataset into different clusters. Here K defines the number of pre-defined clusters that need to be created in the process, as if K=2, there will be two clusters, and for K=3, there will be three clusters, and so on. > It is an iterative algorithm that divides the unlabeled dataset into k different clusters in such a way that each dataset belongs only one group that has similar properties. It allows us to cluster the data into different groups and a convenient way to discover the categories of groups in the unlabeled dataset on its own without the need for any training. It is a centroid-based algorithm, where each cluster is associated with a centroid. The main aim of this algorithm is to minimize the sum of distances between the data point and their corresponding clusters.OOPs Concepts in Java The algorithm takes the unlabeled dataset as input, divides the dataset into k-number of clusters, and repeats the process until it does not find the best clusters. The value of k should be predetermined in this algorithm. The k-means [clustering](https://www.javatpoint.com/clustering-in-machine-learning) algorithm mainly performs two tasks: * Determines the best value for K center points or centroids by an iterative process. * Assigns each data point to its closest k-center. Those data points which are near to the particular k-center, create a cluster. Hence each cluster has datapoints with some commonalities, and it is away from other clusters. The below diagram explains the working of the K-means Clustering Algorithm:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning.png) ### How does the K-Means Algorithm Work? The working of the K-Means algorithm is explained in the below steps: **Step-1:** Select the number K to decide the number of clusters. **Step-2:** Select random K points or centroids. (It can be other from the input dataset). **Step-3:** Assign each data point to their closest centroid, which will form the predefined K clusters. **Step-4:** Calculate the variance and place a new centroid of each cluster. **Step-5:** Repeat the third steps, which means reassign each datapoint to the new closest centroid of each cluster. **Step-6:** If any reassignment occurs, then go to step-4 else go to FINISH. **Step-7**: The model is ready. Let's understand the above steps by considering the visual plots: Suppose we have two variables M1 and M2. The x-y axis scatter plot of these two variables is given below:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning2.png) * Let's take number k of clusters, i.e., K=2, to identify the dataset and to put them into different clusters. It means here we will try to group these datasets into two different clusters. * We need to choose some random k points or centroid to form the cluster. These points can be either the points from the dataset or any other point. So, here we are selecting the below two points as k points, which are not the part of our dataset. Consider the below image:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning3.png) * Now we will assign each data point of the scatter plot to its closest K-point or centroid. We will compute it by applying some mathematics that we have studied to calculate the distance between two points. So, we will draw a median between both the centroids. Consider the below image:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning4.png) From the above image, it is clear that points left side of the line is near to the K1 or blue centroid, and points to the right of the line are close to the yellow centroid. Let's color them as blue and yellow for clear visualization.![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning5.png) * As we need to find the closest cluster, so we will repeat the process by choosing **a new centroid**. To choose the new centroids, we will compute the center of gravity of these centroids, and will find new centroids as below:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning6.png) * Next, we will reassign each datapoint to the new centroid. For this, we will repeat the same process of finding a median line. The median will be like below image:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning7.png) From the above image, we can see, one yellow point is on the left side of the line, and two blue points are right to the line. So, these three points will be assigned to new centroids. ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning8.png) As reassignment has taken place, so we will again go to the step-4, which is finding new centroids or K-points. * We will repeat the process by finding the center of gravity of centroids, so the new centroids will be as shown in the below image:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning9.png) * As we got the new centroids so again will draw the median line and reassign the data points. So, the image will be:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning10.png) * We can see in the above image; there are no dissimilar data points on either side of the line, which means our model is formed. Consider the below image:\ ![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning11.png) As our model is ready, so we can now remove the assumed centroids, and the two final clusters will be as shown in the below image:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning12.png) ### How to choose the value of "K number of clusters" in K-means Clustering? The performance of the K-means clustering algorithm depends upon highly efficient clusters that it forms. But choosing the optimal number of clusters is a big task. There are some different ways to find the optimal number of clusters, but here we are discussing the most appropriate method to find the number of clusters or value of K. The method is given below: #### Elbow Method The Elbow method is one of the most popular ways to find the optimal number of clusters. This method uses the concept of WCSS value. **WCSS** stands for **Within Cluster Sum of Squares**, which defines the total variations within a cluster. The formula to calculate the value of WCSS (for 3 clusters) is given below:WCSS= ∑Pi in Cluster1 distance(Pi C1)2 +∑Pi in Cluster2distance(Pi C2)2+∑Pi in CLuster3 distance(Pi C3)2 In the above formula of WCSS, ∑Pi in Cluster1 distance(Pi C1)2: It is the sum of the square of the distances between each data point and its centroid within a cluster1 and the same for the other two terms. To measure the distance between data points and centroid, we can use any method such as Euclidean distance or Manhattan distance. To find the optimal value of clusters, the elbow method follows the below steps: * It executes the K-means clustering on a given dataset for different K values (ranges from 1-10). * For each value of K, calculates the WCSS value. * Plots a curve between calculated WCSS values and the number of clusters K. * The sharp point of bend or a point of the plot looks like an arm, then that point is considered as the best value of K. Since the graph shows the sharp bend, which looks like an elbow, hence it is known as the elbow method. The graph for the elbow method looks like the below image:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning13.png) **Note: We can choose the number of clusters equal to the given data points. If we choose the number of clusters equal to the data points, then the value of WCSS becomes zero, and that will be the endpoint of the plot.** ### Python Implementation of K-means Clustering Algorithm In the above section, we have discussed the K-means algorithm, now let's see how it can be implemented using [Python](https://www.javatpoint.com/python-tutorial). Before implementation, let's understand what type of problem we will solve here. So, we have a dataset of **Mall\_Customers**, which is the data of customers who visit the mall and spend there. In the given dataset, we have **Customer\_Id, Gender, Age, Annual Income ($), and Spending Score** (which is the calculated value of how much a customer has spent in the mall, the more the value, the more he has spent). From this dataset, we need to calculate some patterns, as it is an unsupervised method, so we don't know what to calculate exactly. The steps to be followed for the implementation are given below: * **Data Pre-processing** * **Finding the optimal number of clusters using the elbow method** * **Training the K-means algorithm on the training dataset** * **Visualizing the clusters** #### Step-1: Data pre-processing Step The first step will be the data pre-processing, as we did in our earlier topics of Regression and Classification. But for the clustering problem, it will be different from other models. Let's discuss it: * **Importing Libraries**\ As we did in previous topics, firstly, we will import the libraries for our model, which is part of data pre-processing. The code is given below: 1. \# importing libraries 2. import numpy as nm 3. import matplotlib.pyplot as mtp 4. import pandas as pd In the above code, the [**numpy**](https://www.javatpoint.com/numpy-tutorial) we have imported for the performing mathematics calculation, **matplotlib** is for plotting the graph, and **pandas** are for managing the dataset. * **Importing the Dataset:**\ Next, we will import the dataset that we need to use. So here, we are using the Mall\_Customer\_data.csv dataset. It can be imported using the below code: 1. \# Importing the dataset 2. dataset = pd.read\_csv('Mall\_Customers\_data.csv') By executing the above lines of code, we will get our dataset in the Spyder IDE. The dataset looks like the below image:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning15.png) From the above dataset, we need to find some patterns in it. * **Extracting Independent Variables** Here we don't need any dependent variable for data pre-processing step as it is a clustering problem, and we have no idea about what to determine. So we will just add a line of code for the matrix of features. 1. x = dataset.iloc\[:, \[3, 4]].values As we can see, we are extracting only 3rd and 4th feature. It is because we need a 2d plot to visualize the model, and some features are not required, such as customer\_id. #### Step-2: Finding the optimal number of clusters using the elbow method In the second step, we will try to find the optimal number of clusters for our clustering problem. So, as discussed above, here we are going to use the elbow method for this purpose. As we know, the elbow method uses the WCSS concept to draw the plot by plotting WCSS values on the Y-axis and the number of clusters on the X-axis. So we are going to calculate the value for WCSS for different k values ranging from 1 to 10. Below is the code for it: 1. \#finding optimal number of clusters using the elbow method 2. from sklearn.cluster import KMeans 3. wcss\_list= \[] #Initializing the list for the values of WCSS 4. 5. \#Using for loop for iterations from 1 to 10. 6. for i in range(1, 11): 7. kmeans = KMeans(n\_clusters=i, init='k-means++', random\_state= 42) 8. kmeans.fit(x) 9. wcss\_list.append(kmeans.inertia\_) 10. mtp.plot(range(1, 11), wcss\_list) 11. mtp.title('The Elobw Method Graph') 12. mtp.xlabel('Number of clusters(k)') 13. mtp.ylabel('wcss\_list') 14. mtp.show() As we can see in the above code, we have used **the KMeans** class of sklearn. cluster library to form the clusters. Next, we have created the **wcss\_list** variable to initialize an empty list, which is used to contain the value of wcss computed for different values of k ranging from 1 to 10. After that, we have initialized the for loop for the iteration on a different value of k ranging from 1 to 10; since for loop in Python, exclude the outbound limit, so it is taken as 11 to include 10th value. The rest part of the code is similar as we did in earlier topics, as we have fitted the model on a matrix of features and then plotted the graph between the number of clusters and WCSS. **Output:** After executing the above code, we will get the below output:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning16.png) From the above plot, we can see the elbow point is at **5. So the number of clusters here will be 5.**![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning17.png) #### Step- 3: Training the K-means algorithm on the training dataset As we have got the number of clusters, so we can now train the model on the dataset. To train the model, we will use the same two lines of code as we have used in the above section, but here instead of using i, we will use 5, as we know there are 5 clusters that need to be formed. The code is given below: 1. \#training the K-means model on a dataset 2. kmeans = KMeans(n\_clusters=5, init='k-means++', random\_state= 42) 3. y\_predict= kmeans.fit\_predict(x) The first line is the same as above for creating the object of KMeans class. In the second line of code, we have created the dependent variable **y\_predict** to train the model. By executing the above lines of code, we will get the y\_predict variable. We can check it under **the variable explorer** option in the Spyder IDE. We can now compare the values of y\_predict with our original dataset. Consider the below image:![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning18.png) From the above image, we can now relate that the CustomerID 1 belongs to a cluster 3(as index starts from 0, hence 2 will be considered as 3), and 2 belongs to cluster 4, and so on. #### Step-4: Visualizing the Clusters The last step is to visualize the clusters. As we have 5 clusters for our model, so we will visualize each cluster one by one. To visualize the clusters will use scatter plot using mtp.scatter() function of matplotlib. 1. \#visulaizing the clusters 2. mtp.scatter(x\[y\_predict == 0, 0], x\[y\_predict == 0, 1], s = 100, c = 'blue', label = 'Cluster 1') #for first cluster 3. mtp.scatter(x\[y\_predict == 1, 0], x\[y\_predict == 1, 1], s = 100, c = 'green', label = 'Cluster 2') #for second cluster 4. mtp.scatter(x\[y\_predict== 2, 0], x\[y\_predict == 2, 1], s = 100, c = 'red', label = 'Cluster 3') #for third cluster 5. mtp.scatter(x\[y\_predict == 3, 0], x\[y\_predict == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4') #for fourth cluster 6. mtp.scatter(x\[y\_predict == 4, 0], x\[y\_predict == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5') #for fifth cluster 7. mtp.scatter(kmeans.cluster\_centers\_\[:, 0], kmeans.cluster\_centers\_\[:, 1], s = 300, c = 'yellow', label = 'Centroid') 8. mtp.title('Clusters of customers') 9. mtp.xlabel('Annual Income (k$)') 10. mtp.ylabel('Spending Score (1-100)') 11. mtp.legend() 12. mtp.show() In above lines of code, we have written code for each clusters, ranging from 1 to 5. The first coordinate of the mtp.scatter, i.e., x\[y\_predict == 0, 0] containing the x value for the showing the matrix of features values, and the y\_predict is ranging from 0 to 1. **Output:**![K-Means Clustering Algorithm](https://static.javatpoint.com/tutorial/machine-learning/images/k-means-clustering-algorithm-in-machine-learning19.png) The output image is clearly showing the five different clusters with different colors. The clusters are formed between two parameters of the dataset; Annual income of customer and Spending. We can change the colors and labels as per the requirement or choice. We can also observe some points from the above patterns, which are given below: * **Cluster1** shows the customers with average salary and average spending so we can categorize these customers as * Cluster2 shows the customer has a high income but low spending, so we can categorize them as **careful**. * Cluster3 shows the low income and also low spending so they can be categorized as sensible. * Cluster4 shows the customers with low income with very high spending so they can be categorized as **careless**. * Cluster5 shows the customers with high income and high spending so they can be categorized as target, and these customers can be the most profitable customers for the mall owner. {% embed url="" %} ### What are some techniques to reduce RAM usage for common ML algorithms? 1. [Sparse Matrix](https://en.wikipedia.org/wiki/Sparse_matrix) is a wonderful way to optimise the data storage. Let’s say you have 10000 columns and 10 million rows in yours dataset, then you would need 10,000,000 \* 10000 bytes for integer storage. That stack for almost 94GB of RAM. Now you might think “Hey how often you get that huge data in ML..I guess it’s not frequent”, then you are absolutely wrong. Try taking the [Amazon Food Review Dataset at Kaggle](https://www.kaggle.com/snap/amazon-fine-food-reviews) for example. If you are trying to predict the polarity of the review and use a techniques like Bag Of Word or Binary Bag of Words or even a [TFIDF](https://en.wikipedia.org/wiki/Tf%E2%80%93idf) bag of Words, the dataset grows so huge that you can't fit it in any place like a normal system. Mostly in text data or image data, the feature set grows so large that you can't store it anywhere. But fortunately most machine learning algorithms can use sparse matrix as an input and hence you can save a hell lot of storage. Mostly it depends on the sparsity of the data but typically a dense matrix of 100GB can be stored into just 700 to 900 MB if using sparse matrix. The biggest shortcoming is that if in your data you have less numbers of repeated values or in fact no repeated values at all, the memory footprint of a sparse and dense matrix becomes almost same and it’s of no use but this scenario itself is very rare. 2. [Partial Fit](https://stackoverflow.com/questions/24617356/sklearn-sgdclassifier-partial-fit) on the dataset if it is so big to fit in one go. This feature allows you to fit a model on the data partially step by step instead of fitting in one go. So it takes some data fit on that data to get say a weight vector and then it moves to the next part of the data and fit again on the existing weight vector and so on. Needless to say that this decreases the RAM consumption but increases the training time. The biggest shortcoming is not all the algorithms and their implementations use partial fit. 3. Using right algorithms can save you a lot of hassle. Some algorithms might have large memory requirement as compared to others. This is not during the training time but this is during the runtime. For example, [KNN](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html) requires to store all the data points to predict during the runtime and even with some of the optimisations like [KDTree](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KDTree.html#sklearn.neighbors.KDTree) or [BallTree](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.BallTree.html#sklearn.neighbors.BallTree) or LSH with KNN, runtime memory requirement is huge while if you are using something say like [Naive Bayes](http://scikit-learn.org/stable/modules/naive_bayes.html) the runtime space complexity is only O(d \* k)..while d is number of features and k is number of class labels. This is far more lesser than O(n) for n = number of data points most of the times. Logistic regression on the other hand has even better runtime space complexity of O(d). So better use logistic regression against Naive Bayes. 4. [Dimensionality Reduction](https://en.wikipedia.org/wiki/Dimensionality_reduction) is not only useful to reduce the training time but also memory consumption during the runtime. Using some techniques like [PCA](https://en.wikipedia.org/wiki/Dimensionality_reduction#Principal_component_analysis_\(PCA\)) or [LDA](https://en.wikipedia.org/wiki/Linear_discriminant_analysis) or [Matrix Factorization](https://en.wikipedia.org/wiki/Dimensionality_reduction#Non-negative_matrix_factorization_\(NMF\)) can reduce the dimensionality dramatically and sometime super useful. 5. A smart technique during cross validation can be performed on the Random Stratified Samples of size m which is far lesser than actual data size n that can give you a decent performing weight vector which might not help you win a Kaggle Championship but it is good for most production environments. ## Machine Learning with Kaggle: Feature Engineering Learn how feature engineering can help you to up your game when building machine learning models in Kaggle: create new columns, transform variables and more! In the two previous Kaggle tutorials, you learned all about how to get your data in a form to build your first machine learning model, using [Exploratory Data Analysis and baseline machine learning models](https://www.datacamp.com/community/tutorials/kaggle-machine-learning-eda). Next, you successfully managed to [build your first machine learning model](https://www.datacamp.com/community/tutorials/kaggle-tutorial-machine-learning), a decision tree classifier. You submitted all these models to Kaggle and interpreted their accuracy. In this third tutorial, you'll learn more about feature engineering, a process where you use domain knowledge of your data to create additional relevant features that increase the predictive power of the learning algorithm and make your machine learning models perform even better! More specifically, * You'll first [get started](https://www.datacamp.com/community/tutorials/feature-engineering-kaggle#start) by doing all necessary imports and getting the data in your workspace; * Then, you'll see some reasons why you should do [feature engineering](https://www.datacamp.com/community/tutorials/feature-engineering-kaggle#feature) and start working on engineering your own new features for your data set! You'll create new columns, transform variables into numerical ones, handle missing values, and much more. * Lastly, you'll [build a new machine learning model](https://www.datacamp.com/community/tutorials/feature-engineering-kaggle#ml) with your new data set and submit it to Kaggle. ### Getting Started! Before you can start off, you're going to do all the imports, just like you did in the previous tutorial, use some IPython magic to make sure the figures are generated inline in the Jupyter Notebook and set the visualization style. Next, you can import your data and make sure that you store the target variable of the training data in a safe place. Afterwards, you merge the train and test data sets (with exception of the `'Survived'` column of `df_train`) and store the result in `data`. **Remember** that you do this because you want to make sure that any preprocessing that you do on the data is reflected in both the train and test sets! Lastly, you use the `.info()` method to take a look at your data: ``` # Imports import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import re import numpy as np from sklearn import tree from sklearn.model_selection import GridSearchCV # Figures inline and set visualization style %matplotlib inline sns.set() # Import data df_train = pd.read_csv('data/train.csv') df_test = pd.read_csv('data/test.csv') # Store target variable of training data in a safe place survived_train = df_train.Survived # Concatenate training and test sets data = pd.concat([df_train.drop(['Survived'], axis=1), df_test]) # View head data.info() ``` ``` Int64Index: 1309 entries, 0 to 417 Data columns (total 11 columns): PassengerId 1309 non-null int64 Pclass 1309 non-null int64 Name 1309 non-null object Sex 1309 non-null object Age 1046 non-null float64 SibSp 1309 non-null int64 Parch 1309 non-null int64 Ticket 1309 non-null object Fare 1308 non-null float64 Cabin 295 non-null object Embarked 1307 non-null object dtypes: float64(2), int64(4), object(5) memory usage: 122.7+ KB ``` ### Why Feature Engineer At All? You perform feature engineering to extract more information from your data, so that you can up your game when building models. #### Titanic's Passenger Titles Let's check out what this is all about by looking at an example. Let's check out the `'Name'` column with the help of the `.tail()` method, which helps you to see the last five rows of your data: ``` # View head of 'Name' column data.Name.tail() ``` ``` 413 Spector, Mr. Woolf 414 Oliva y Ocana, Dona. Fermina 415 Saether, Mr. Simon Sivertsen 416 Ware, Mr. Frederick 417 Peter, Master. Michael J Name: Name, dtype: object ``` Suddenly, you see different titles emerging! In other words, this column contains strings or text that contain titles, such as 'Mr', 'Master' and 'Dona'. These titles of course give you information on social status, profession, etc., which in the end could tell you something more about survival. At first sight, it might seem like a difficult task to separate the names from the titles, but don't panic! Remember, you can easily use regular expressions to extract the title and store it in a new column `'Title'`: ``` # Extract Title from Name, store in column and plot barplot data['Title'] = data.Name.apply(lambda x: re.search(' ([A-Z][a-z]+)\.', x).group(1)) sns.countplot(x='Title', data=data); plt.xticks(rotation=45); ``` ![](http://res.cloudinary.com/dyd911kmh/image/upload/f_auto,q_auto:best/v1515151833/output_5_0_d77zb9.png) **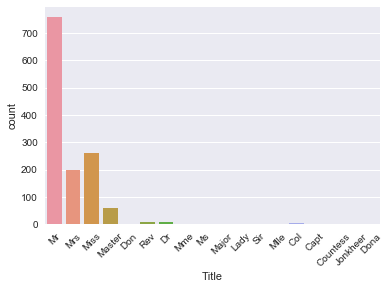Note** that this new column `'Title'` is actually a new feature for your data set! **Tip**: to learn more about regular expressions, check out my write up of our last [FB Live code along event](https://www.datacamp.com/community/tutorials/web-scraping-python-nlp) or check out DataCamp's [Python Regular Expressions Tutorial](https://www.datacamp.com/community/tutorials/python-regular-expression-tutorial). You can see that there are several titles in the above plot and there are many that don't occur so often. So, it makes sense to put them in fewer buckets. For example, you probably want to replace `'Mlle'` and `'Ms'` with `'Miss'` and `'Mme'` by `'Mrs'`, as these are French titles and ideally, you want all your data to be in one language. Next, you also take a bunch of titles that you can't immediately categorize and put them in a bucket called `'Special'`. **Tip**: play around with this to see how your algorithm performs as a function of it! Next, you view a barplot of the result with the help of the `.countplot()` method: ``` data['Title'] = data['Title'].replace({'Mlle':'Miss', 'Mme':'Mrs', 'Ms':'Miss'}) data['Title'] = data['Title'].replace(['Don', 'Dona', 'Rev', 'Dr', 'Major', 'Lady', 'Sir', 'Col', 'Capt', 'Countess', 'Jonkheer'],'Special') sns.countplot(x='Title', data=data); plt.xticks(rotation=45); ``` ![](http://res.cloudinary.com/dyd911kmh/image/upload/f_auto,q_auto:best/v1515151833/output_7_0_vdtvcz.png) 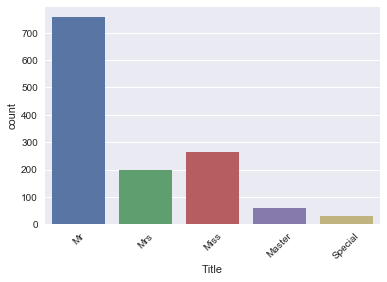This is what your newly engineered feature `'Title'` looks like! Now, make sure that you have a `'Title'` column and check out your data again with the `.tail()` method: ``` # View head of data data.tail() ``` | | PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | Title | | --- | ----------- | ------ | ---------------------------- | ------ | ---- | ----- | ----- | ------------------ | -------- | ----- | -------- | ------- | | 413 | 1305 | 3 | Spector, Mr. Woolf | male | NaN | 0 | 0 | A.5. 3236 | 8.0500 | NaN | S | Mr | | 414 | 1306 | 1 | Oliva y Ocana, Dona. Fermina | female | 39.0 | 0 | 0 | PC 17758 | 108.9000 | C105 | C | Special | | 415 | 1307 | 3 | Saether, Mr. Simon Sivertsen | male | 38.5 | 0 | 0 | SOTON/O.Q. 3101262 | 7.2500 | NaN | S | Mr | | 416 | 1308 | 3 | Ware, Mr. Frederick | male | NaN | 0 | 0 | 359309 | 8.0500 | NaN | S | Mr | | 417 | 1309 | 3 | Peter, Master. Michael J | male | NaN | 1 | 1 | 2668 | 22.3583 | NaN | C | Master | #### Passenger's Cabins When you loaded in the data and inspected it, you saw that there are several `NaN`s or missing values in the `'Cabin'` column. It is reasonable to presume that those `NaN`s didn't have a cabin, which could tell you something about `'Survival'`. So, let's now create a new column `'Has_Cabin'` that encodes this information and tells you whether passengers had a cabin or not. **Note** that you use the `.isnull()` method in the code chunk below, which will return `True` if the passenger doesn't have a cabin and `False` if that's not the case. However, since you want to store the result in a column `'Has_Cabin'`, you actually want to flip the result: you want to return `True` if the passenger has a cabin. That's why you use the tilde `~`. ``` # Did they have a Cabin? data['Has_Cabin'] = ~data.Cabin.isnull() # View head of data data.head() ``` | | PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | Title | Has\_Cabin | | - | ----------- | ------ | ------------------------------------------------- | ------ | ---- | ----- | ----- | ---------------- | ------- | ----- | -------- | ----- | ---------- | | 0 | 1 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S | Mr | False | | 1 | 2 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C | Mrs | True | | 2 | 3 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S | Miss | False | | 3 | 4 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S | Mrs | True | | 4 | 5 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S | Mr | False | What you want to do now is drop a bunch of columns that contain no more useful information (or that we're not sure what to do with). In this case, you're looking at columns such as `['Cabin', 'Name', 'PassengerId', 'Ticket']`, because * You already extracted information on whether or not the passenger had a cabin in your newly added `'Has_Cabin'` column; * Also, you already extracted the titles from the `'Name'` column; * You also drop the `'PassengerId'` and the `'Ticket'` columns because these will probably not tell you anything more about the survival of the Titanic passengers. **Tip** there might be more information in the `'Cabin'` column, but for this tutorial, you assume that there isn't! To drop these columns in your actual `data` DataFrame, make sure to use the `inplace` argument in the `.drop()` method and set it to `True`: ``` # Drop columns and view head data.drop(['Cabin', 'Name', 'PassengerId', 'Ticket'], axis=1, inplace=True) data.head() ``` | | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | Has\_Cabin | | - | ------ | ------ | ---- | ----- | ----- | ------- | -------- | ----- | ---------- | | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S | Mr | False | | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C | Mrs | True | | 2 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S | Miss | False | | 3 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S | Mrs | True | | 4 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S | Mr | False | Congrats! You've successfully engineered some new features such as `'Title'` and `'Has_Cabin'` and made sure that features that don't add any more useful information for your machine learning model are now dropped from your DataFrame! Next, you want to deal with deal with missing values, bin your numerical data, and transform all features into numeric variables using `.get_dummies()` again. Lastly, you'll build your final model for this tutorial. Check out how all of this is done in the next sections! #### Handling Missing Values With all of the changes you have made to your original `data` DataFrame, it's a good idea to figure out if there are any missing values left with `.info()`: ``` data.info() ``` ``` Int64Index: 1309 entries, 0 to 417 Data columns (total 9 columns): Pclass 1309 non-null int64 Sex 1309 non-null object Age 1046 non-null float64 SibSp 1309 non-null int64 Parch 1309 non-null int64 Fare 1308 non-null float64 Embarked 1307 non-null object Title 1309 non-null object Has_Cabin 1309 non-null bool dtypes: bool(1), float64(2), int64(3), object(3) memory usage: 133.3+ KB ``` The result of the above line of code tells you that you have missing values in `'Age'`, `'Fare'`, and `'Embarked'`. **Remember** that you can easily spot this by first looking at the total number of entries (1309) and then checking out the number of non-null values in the columns that `.info()` lists. In this case, you see that `'Age'` has 1046 non-null values, so that means that you have 263 missing values. Similarly, `'Fare'` only has one missing value and `'Embarked'` has two missing values. Just like you did in the previous tutorial, you're going to impute these missing values with the help of `.fillna()`: **Note** that, once again, you use the median to fill in the `'Age'` and `'Fare'` columns because it's perfect for dealing with outliers. Other ways to impute missing values would be to use the mean, which you can find by adding all data points and dividing by the number of data points, or mode, which is the number that occurs the highest number of times. You fill in the two missing values in the `'Embarked'` column with `'S'`, which stands for Southampton, because this value is the most common one out of all the values that you find in this column. **Tip**: you can double check this by doing some more Exploratory Data Analysis! ``` # Impute missing values for Age, Fare, Embarked data['Age'] = data.Age.fillna(data.Age.median()) data['Fare'] = data.Fare.fillna(data.Fare.median()) data['Embarked'] = data['Embarked'].fillna('S') data.info() ``` ``` Int64Index: 1309 entries, 0 to 417 Data columns (total 9 columns): Pclass 1309 non-null int64 Sex 1309 non-null object Age 1309 non-null float64 SibSp 1309 non-null int64 Parch 1309 non-null int64 Fare 1309 non-null float64 Embarked 1309 non-null object Title 1309 non-null object Has_Cabin 1309 non-null bool dtypes: bool(1), float64(2), int64(3), object(3) memory usage: 133.3+ KB ``` ``` data.head() ``` | | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | Has\_Cabin | | - | ------ | ------ | ---- | ----- | ----- | ------- | -------- | ----- | ---------- | | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S | Mr | False | | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C | Mrs | True | | 2 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S | Miss | False | | 3 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S | Mrs | True | | 4 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S | Mr | False | #### Bin numerical data Next, you want to bin the numerical data, because you have a range of ages and fares. However, there might be fluctuations in those numbers that don't reflect patterns in the data, which might be noise. That's why you'll put people that are within a certain range of age or fare in the same bin. You can do this by using the `pandas` function `qcut()` to bin your numerical data: ``` # Binning numerical columns data['CatAge'] = pd.qcut(data.Age, q=4, labels=False ) data['CatFare']= pd.qcut(data.Fare, q=4, labels=False) data.head() ``` | | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | Has\_Cabin | CatAge | CatFare | | - | ------ | ------ | ---- | ----- | ----- | ------- | -------- | ----- | ---------- | ------ | ------- | | 0 | 3 | male | 22.0 | 1 | 0 | 7.2500 | S | Mr | False | 0 | 0 | | 1 | 1 | female | 38.0 | 1 | 0 | 71.2833 | C | Mrs | True | 3 | 3 | | 2 | 3 | female | 26.0 | 0 | 0 | 7.9250 | S | Miss | False | 1 | 1 | | 3 | 1 | female | 35.0 | 1 | 0 | 53.1000 | S | Mrs | True | 2 | 3 | | 4 | 3 | male | 35.0 | 0 | 0 | 8.0500 | S | Mr | False | 2 | 1 | **Note** that you pass in the data as a Series, `data.Age` and `data.Fare`, after which you specify the number of quantiles, `q=4`. Lastly, you set the `labels` argument to `False` to encode the bins as numbers. Now that you have all of that information in bins, you can now safely drop `'Age'` and `'Fare'` columns. Don't forget to check out the first five rows of your data! ``` data = data.drop(['Age', 'Fare'], axis=1) data.head() ``` | | Pclass | Sex | SibSp | Parch | Embarked | Title | Has\_Cabin | CatAge | CatFare | | - | ------ | ------ | ----- | ----- | -------- | ----- | ---------- | ------ | ------- | | 0 | 3 | male | 1 | 0 | S | Mr | False | 0 | 0 | | 1 | 1 | female | 1 | 0 | C | Mrs | True | 3 | 3 | | 2 | 3 | female | 0 | 0 | S | Miss | False | 1 | 1 | | 3 | 1 | female | 1 | 0 | S | Mrs | True | 2 | 3 | | 4 | 3 | male | 0 | 0 | S | Mr | False | 2 | 1 | ### Number of Members in Family Onboard The next thing you can do is create a new column, which is the number of members in families that were onboard of the Titanic. In this tutorial, you won't go in this and see how the model performs without it. If you do want to check out how the model would do with this additional column, run the following line of code: ``` # Create column of number of Family members onboard data['Fam_Size'] = data.Parch + data.SibSp ``` For now, you will just go ahead and drop the `'SibSp'` and `'Parch'` columns from your DataFrame: ``` # Drop columns data = data.drop(['SibSp','Parch'], axis=1) data.head() ``` | | Pclass | Sex | Embarked | Title | Has\_Cabin | CatAge | CatFare | | - | ------ | ------ | -------- | ----- | ---------- | ------ | ------- | | 0 | 3 | male | S | Mr | False | 0 | 0 | | 1 | 1 | female | C | Mrs | True | 3 | 3 | | 2 | 3 | female | S | Miss | False | 1 | 1 | | 3 | 1 | female | S | Mrs | True | 2 | 3 | | 4 | 3 | male | S | Mr | False | 2 | 1 | ### Transform Variables into Numerical Variables Now that you have engineered some more features, such as `'Title'` and `'Has_Cabin'`, and you have dealt with missing values, binned your numerical data, it's time to transform all variables into numeric ones. You do this because machine learning models generally take numeric input. As you have done previously, you will use `.get_dummies()` to do this: ``` # Transform into binary variables data_dum = pd.get_dummies(data, drop_first=True) data_dum.head() ``` | | Pclass | Has\_Cabin | CatAge | CatFare | Sex\_male | Embarked\_Q | Embarked\_S | Title\_Miss | Title\_Mr | Title\_Mrs | Title\_Special | | - | ------ | ---------- | ------ | ------- | --------- | ----------- | ----------- | ----------- | --------- | ---------- | -------------- | | 0 | 3 | False | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | | 1 | 1 | True | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | | 2 | 3 | False | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | | 3 | 1 | True | 2 | 3 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | | 4 | 3 | False | 2 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | With all of this done, it's time to build your final model! ### Building models with Your New Data Set! As before, you'll first split your `data` back into training and test sets. Then, you'll transform them into arrays: ``` # Split into test.train data_train = data_dum.iloc[:891] data_test = data_dum.iloc[891:] # Transform into arrays for scikit-learn X = data_train.values test = data_test.values y = survived_train.values ``` You're now going to build a decision tree on your brand new feature-engineered dataset. To choose your hyperparameter `max_depth`, you'll use a variation on test train split called "cross validation". 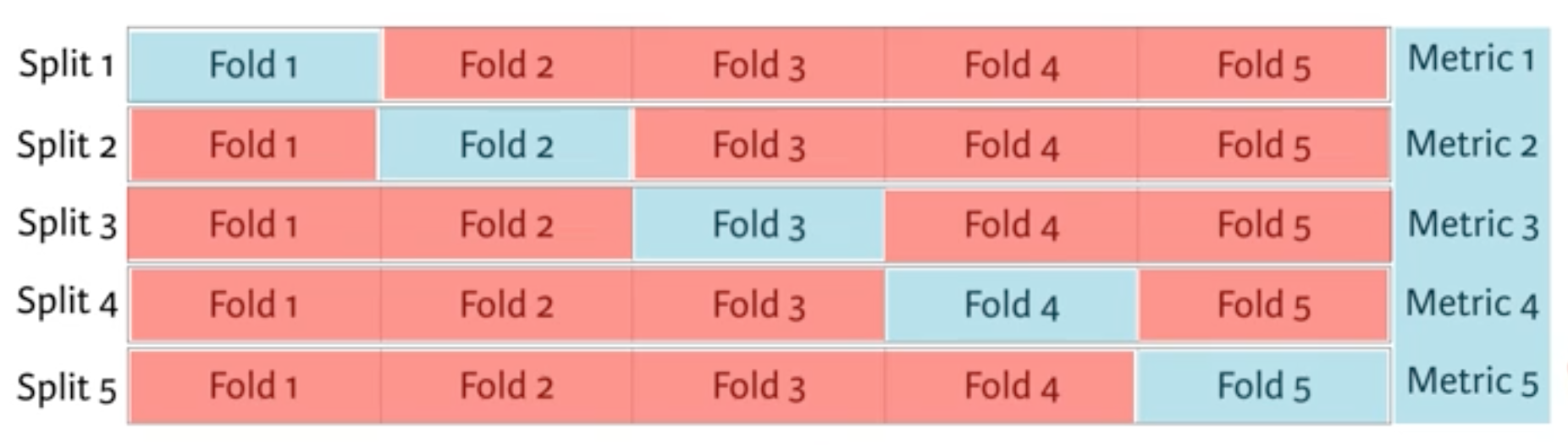![](http://res.cloudinary.com/dyd911kmh/image/upload/f_auto,q_auto:best/v1514303215/cv_raxrt7.png) You begin by splitting the dataset into 5 groups or *folds*. Then you hold out the first fold as a test set, fit your model on the remaining four folds, predict on the test set and compute the metric of interest. Next, you hold out the second fold as your test set, fit on the remaining data, predict on the test set and compute the metric of interest. Then similarly with the third, fourth and fifth. As a result, you get five values of accuracy, from which you can compute statistics of interest, such as the median and/or mean and 95% confidence intervals. You do this for each value of each hyperparameter that you're tuning and choose the set of hyperparameters that performs the best. This is called *grid search*. Enough about that for now, let's get it! In the following, you'll use cross validation and grid search to choose the best `max_depth` for your new feature-engineered dataset: ``` # Setup the hyperparameter grid dep = np.arange(1,9) param_grid = {'max_depth' : dep} # Instantiate a decision tree classifier: clf clf = tree.DecisionTreeClassifier() # Instantiate the GridSearchCV object: clf_cv clf_cv = GridSearchCV(clf, param_grid=param_grid, cv=5) # Fit it to the data clf_cv.fit(X, y) # Print the tuned parameter and score print("Tuned Decision Tree Parameters: {}".format(clf_cv.best_params_)) print("Best score is {}".format(clf_cv.best_score_)) ``` ``` Tuned Decision Tree Parameters: {'max_depth': 3} Best score is 0.8103254769921436 ``` Now, you can make predictions on your test set, create a new column `'Survived'` and store your predictions in it. Don't forget to save the `'PassengerId'` and `'Survived'` columns of `df_test` to a .csv and submit it to Kaggle! 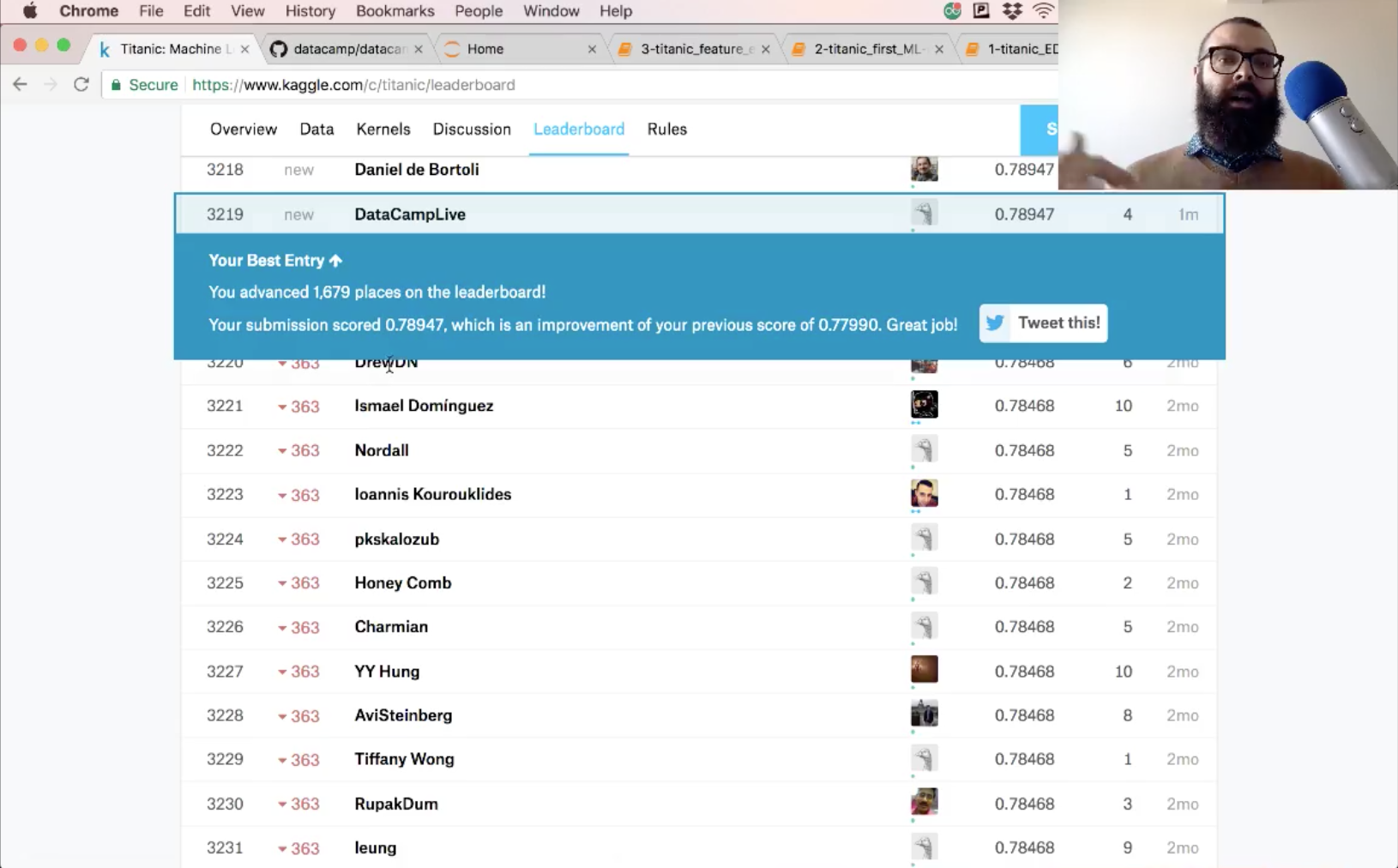``` Y_pred = clf_cv.predict(test) df_test['Survived'] = Y_pred df_test[['PassengerId', 'Survived']].to_csv('data/predictions/dec_tree_feat_eng.csv', index=False) ``` ![](http://res.cloudinary.com/dyd911kmh/image/upload/f_auto,q_auto:best/v1515168392/Screen_Shot_2018-01-05_at_17.05.05_nrg93w.png) The accuracy of your submission is 78.9. {% embed url="" %} #### .